多相反应流在能源与动力工程、化学工程、环境工程等领域广泛存在。气固湍流燃烧过程是一个存在着多场耦合及时空多尺度结构的复杂体系，无论是对常规燃烧方式的优化和控制、还是对新型燃烧技术的设计和放大，均特别依赖于对其内部相互耦合的多相流场、温度场、组分场的理解和对内部复杂物理化学过程的认识。

介尺度是由大量单元组成的系统在全局与个体之间的尺度上形成的复杂时空结构，它主要表现在分子到颗粒间的材料表界面时空尺度、以及颗粒到反应器整体间的颗粒聚团时空尺度，这也是我们的研究焦点。

多相反应流模型与方法方面的主要研究工作包括：

       (1) 气固两相流的雷诺应力-拉氏PDF模型

• 对流体相采用基于雷诺平均Navier-Stokes(RANS)的二阶矩模型、对于颗粒相运动采用拉氏PDF(概率密度函数)模型、对于颗粒碰撞采用直接模拟Monte Carlo(DSMC)，实现四向耦合。我们发展了这种流体-轨道模型，并对轴对称气固射流等进行宏观模拟。

• 
  

SOM-PDF-DSMC模拟突扩有旋气粒两相流场: 颗粒轴向平均速度(左)和脉动速度(右)

参考文献：

1. Yongxiang He, Haibo Zhao^*. Conservative particle weighting scheme for particle collision in gas-solid flows. International Journal of Multiphase Flows, 2016, 83: 12-26

2. Yongxiang He, Haibo Zhao^*, Haoming Wang, Chuguang Zheng. Differentially-weighted direct simulation Monte Carlo for particle collision in gas-solid flows. Particuology, 2015, 21: 135-145

(2) 细颗粒流的格子Boltzmann-元胞自动机概率模型

• 这是一种介观层面的气固两相流模型，其特点是虚拟流体颗粒和固体颗粒均限制在同一套规则格点上运动，具有便于考虑两相相互作用、易于实现并行计算、处理复杂边界条件、考虑细颗粒运动随机本质等特点。也通过直接模拟Monte Carlo方法耦合、可考虑颗粒碰撞，实现四相耦合。我们提出了这种格子Boltzmann-元胞自动机概率模型，用于后台阶气固两相流、纤维捕集细微颗粒物等数值模拟。

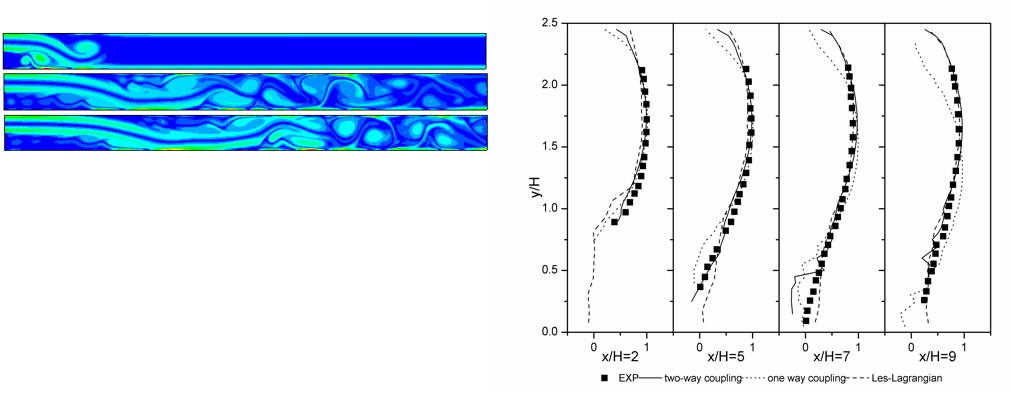
格子Boltzmann-元胞自动机概率模型模拟后台阶气固两相流工况 (左：涡量演变；右：颗粒流向平均速度)

参考文献:

1. Haoming Wang, Haibo Zhao*, Zhaoli Guo, et al. Lattice Boltzmann method for simulations of gas-particle flows over a backward-facing step. Journal of Computational Physics, 2013, 239: 57-71

2. Haoming Wang, Haibo Zhao^*, Zhaoli Guo, Chuguang Zheng. Numerical Simulation of Particle Capture Process of Fibrous Filters using Lattice Boltzmann Two-phase Flow Model. Powder Technology, 2012, 227: 111–122

     (3) 颗粒动力学演变的颗粒群平衡模拟-Monte Carlo(PBMC)方法

• 多相反应流数值模拟不仅需要考虑传统的质量平衡、动量平衡、能量平衡和化学反应(三传一反)，还往往需要考虑颗粒数密度及其重要的内部变量(如碰撞半径、表面积、组分等)的平衡关系—称为“颗粒群平衡”，这对于细微颗粒物的动力学演变过程(包括颗粒碰撞、团聚、烧结、破碎、冷凝/蒸发、成核、沉积、表面化学反应等)尤其重要。颗粒群平衡模拟定量描述各种动力学事件主导下颗粒群内部变量分布函数的时间演变和空间扩散过程，不仅可以单独研究流体颗粒系统的复杂动力学演变过程，也可以与常规多相反应流模型耦合起来模拟连续相-离散相、离散相-离散相间的相互作用。我们提出了符合物理本质的异权值模拟颗粒凝并/团聚模型，发展了多种异权值模拟颗粒凝并准则，据此设计了多套PBMC方法，并通过实现单重遍历模拟颗粒凝并/团聚、GPU并行计算等加速模拟，通过模拟过程调整异权值模拟颗粒尺度分布尽可能均匀而改善随机统计早上，由此构建了高效高精度的颗粒群平衡模拟异权值Monte Carlo方法。在此基础上，与模拟(气固)流体动力学的CFD耦合起来，实现CFD-PBMC模拟。

• 
  

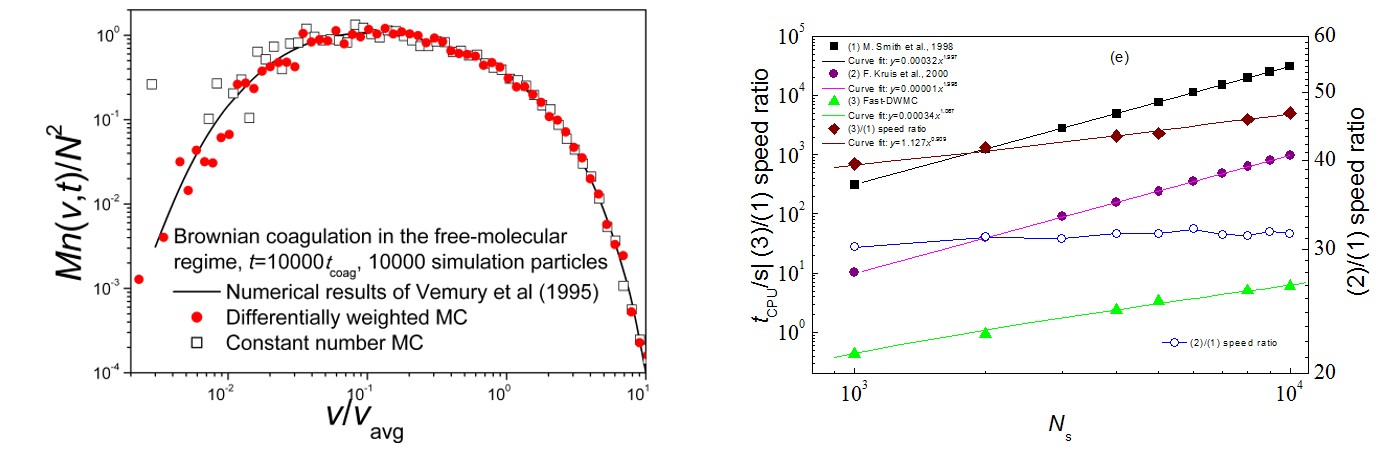
颗粒群平衡模拟异权值Monte Carlo方法与国际同类方法关于精度(左图)和效率(图右)的比较

参考文献：

1. 赵海波*, 郑楚光. 离散系统动力学演变过程的颗粒群平衡模拟. 北京：科学出版社, 2008

2. Zuwei Xu, Haibo Zhao^*, Chuguang Zheng. Accelerating population balance-Monte Carlo simulation for coagulation dynamics from the Markov jump model, stochastic algorithm and GPU parallel computing. Journal of Computational Physics, 2015, 281: 844-863

3. Haibo Zhao^*, F. Einar Kruis, Chuguang Zheng. A differentially weighted Monte Carlo method for two-component coagulation. Journal of Computational Physics, 2010, 229, 6931-6945

4. Haibo Zhao, Chuguang Zheng. A new event-driven constant volume method for solution of the time evolution of particle size distribution. Journal of Computational Physics, 2009, 228(5): 1412-1428.

5. Haibo Zhao^*, F. Einar Kruis^*, Chuguang Zheng. Reducing Statistical Noise and Extending the Size Spectrum by Applying Weighted Simulation Particles in Monte Carlo Simulation of Coagulation. Aerosol Science and Technology, 2009, 43(8): 781-793.

6. Haibo Zhao^*, Chuguang Zheng, Minghou Xu. Multi-Monte Carlo method for coagulation and condensation/evaporation in dispersed systems. Journal of Colloid and Interface Science, 2005, 286(1): 195-208

7. Zuwei Xu, Haibo Zhao^*, Chuguang Zheng. Fast Monte Carlo simulation for particle coagulation in population balance. Journal of Aerosol Science, 2014, 74, 11-25

8. Haibo Zhao^*, Chuguang Zheng. Correcting the multi-Monte Carlo method for particle coagulation. Powder Technology, 2009, 193: 120–123

9. Haibo Zhao^*, Arkadi Maisels^*, Themis Matsoukas^*, Chuguang Zheng. Analysis of four popular Monte Carlo methods for solution of population balances in dispersed systems. Powder Technology, 2007, 173(1): 38-50

10. Haibo Zhao^*, Chuguang Zheng, Minghou Xu. Multi-Monte Carlo approach for general dynamic equation considering simultaneous particle coagulation and breakage. Powder Technology, 2005, 154(2-3): 164-178

11. Haibo Zhao^*, Chuguang Zheng. A population balance-Monte Carlo method for particle coagulation in spatially inhomogeneous systems. Computers & Fluids, 2013, 71: 196–207

 (4) 颗粒动力学事件核模型

•   颗粒群平衡模拟中，动力学事件的速率模型(核模型)是对颗粒群动力学演变过程进行宏观模拟的关键。烧结事件通过团聚体表面积以指数形式变化这一特性来描述，其中最为重要的模型为特征烧结时间。通过耦合PBMC和反问题算法来辨识特征烧结时间模型中的两个不确定参数（指前因子A及活化能E），发现指前因子和活化能存在类Arrhenius关系，且两个不确定参数之间存在线性补偿关系。针对纳米颗粒高温环境中的晶相转变问题，建立了单颗粒线性缩核相变模型，这样可将晶相转变动力学模型纳入颗粒群平衡随机模拟（PBMC）框架。

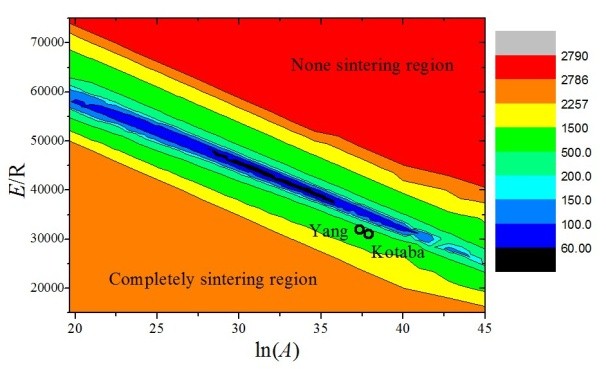
    烧结机理参数的反问题辨识

   

参考文献：

1. Xiaoming Hao, Haibo Zhao^*, Zuwei Xu, Chuguang Zheng. Identification of the compensation effect in the characteristic sintering time model for population balances. Journal of Aerosol Science, 2015, 82: 1-12

2. Zuwei Xu, Hanqing Zhao, Haibo Zhao^*. CFD-population balance Monte Carlo simulation and numerical optimization for flame synthesis of TiO₂ nanoparticles. Proceedings of the Combustion Institute, 2017, 36(1): 1099-1108

(5) 非均匀颗粒聚团的多尺度曳力模型(方法)

• 快速流化床内团聚体的形成导致传统的均匀化曳力模型不适用于描述快速流化床内气固相间流动，对快速床内非均匀结构进行正确描述的关键在于对团聚体边界的合理描述，因为在团聚体的边界处颗粒浓度分布呈现出最大的非均匀性，这种非均匀性导致颗粒所受平均曳力小于均匀分布状态下颗粒所受到的平均曳力。由于固体体积分数梯度是分辨团聚体颗粒边界上非均匀性的特征物理量，为此我们以固体体积分数梯度作为自变量来修正均匀化曳力模型，使无量纲曳力成为颗粒雷诺数、固体体积分数和固体体积分数梯度的三元函数，从而提出你基于网格内固体体积分数梯度修正的多尺度曳力模型。通过对本模型与气固流动网格过滤理论之间的相容性分析，发现两者之间不但有良好的相容性，而且本模型可以视为过滤理论的一种封闭形式。该多尺度曳力模型可以通过CFD模拟软件的UDF(用户自定义函数)轻易实现，且并不明显增加计算效率。通过一个二维提升管的CFD模拟验证了本模型的适用性，模拟结果与实验结果吻合良好。

       

    

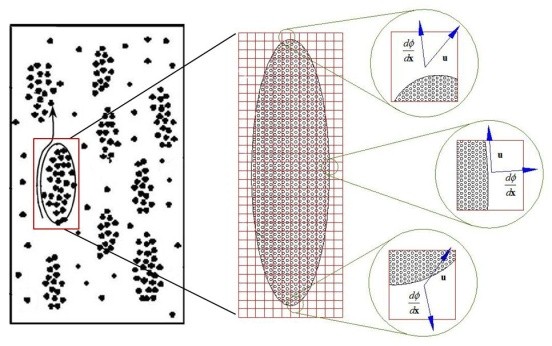
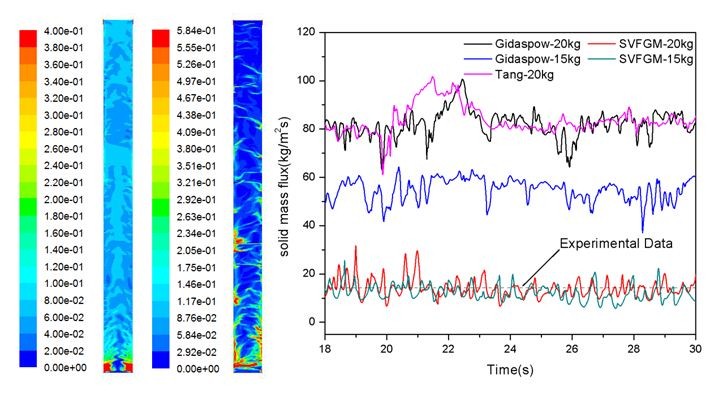
多尺度曳力模型示意图(左)、提升管内固体体积分数瞬时分布和提升管出口固体质量流率：Gidaspow模型、多尺度曳力模型以及实验结果的比较

参考文献：

1. Mingze Su, Haibo Zhao*. Modifying the interphase drag via solid volume fraction gradient for CFD simulation of gas-solid flows in fast fluidized beds. AIChE Journal, 2017, 63(7): 2588-2598

在多相反应流数值模拟与应用方面的研究工作主要包括：

 (6) 自然环境下可吸入颗粒物沉降过程的PBMC模拟

• 为了借鉴大自然的自身净化机制而发展燃煤可吸入颗粒物(PM)的高效除尘方案，以及研究燃煤除尘器出口PM在自然环境中的生命历程，利用颗粒群平衡随机模拟对自然环境中气溶胶颗粒物的干沉降和湿沉降过程进行了定量描述。

• 
  

     

     

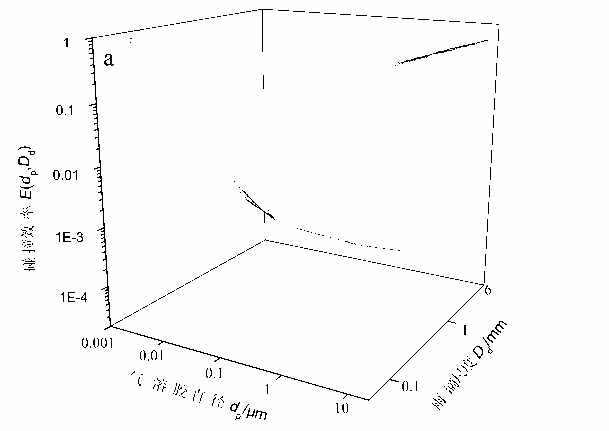
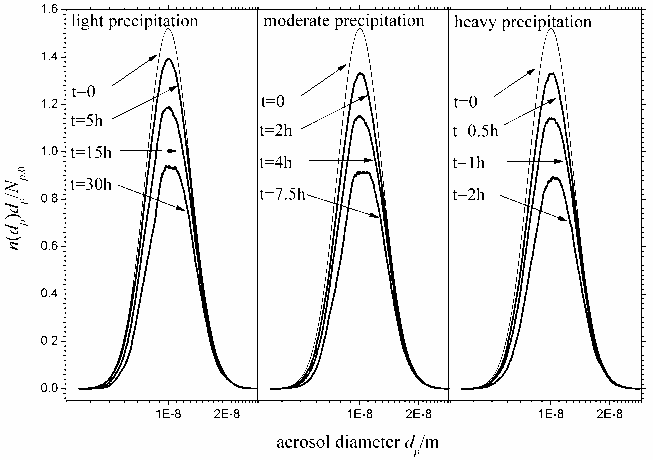
降雨过程中雨滴捕集气溶胶颗粒的机理分析(左图)和降雨条件对气溶胶湿沉降效果的影响(右图)

参考文献：

1. Haibo Zhao^*, Chuguang Zheng. Monte Carlo solution of wet removal of aerosols by precipitation. Atmospheric Environment，2006, 40(8): 1510-1525

2. Haibo Zhao^*, Chuguang Zheng. Stochastic algorithm and numerical simulation for drop scavenging of aerosols. Applied Mathematics and Mechanics-English Edition, 2006, 27(10): 1321-1332

(7) 典型除尘装置中可吸入颗粒物捕集过程的PBMC模拟

• 对常规除尘器(静电除尘器、重力喷淋湿式除尘器、静电增强湿式除尘器和电袋除尘器)捕集颗粒过程进行颗粒群平衡模拟，探究燃煤PM在各种外场作用下(电场、重力场、液滴碰撞捕集、纤维拦截捕集等)的动力学演变细节信息和生命历程，研究颗粒物(特别是0.1~1μm区间的细微颗粒)的捕集机理，确定了新型除尘技术的若干优化参数和敏感参数，并指导传统除尘技术的运行优化和高效改进。

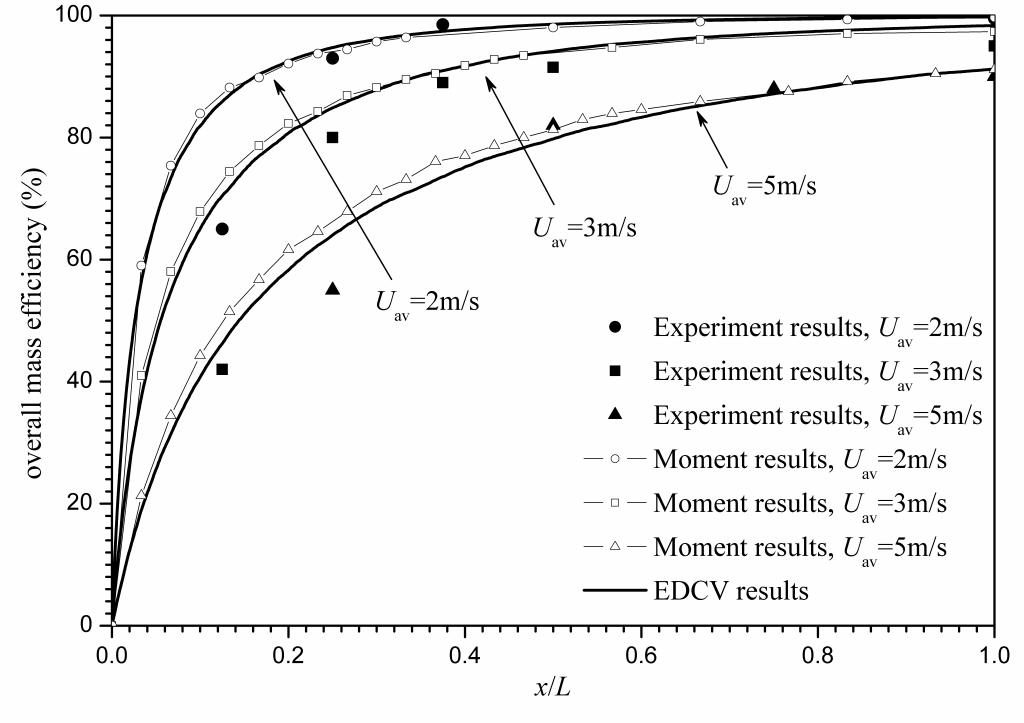
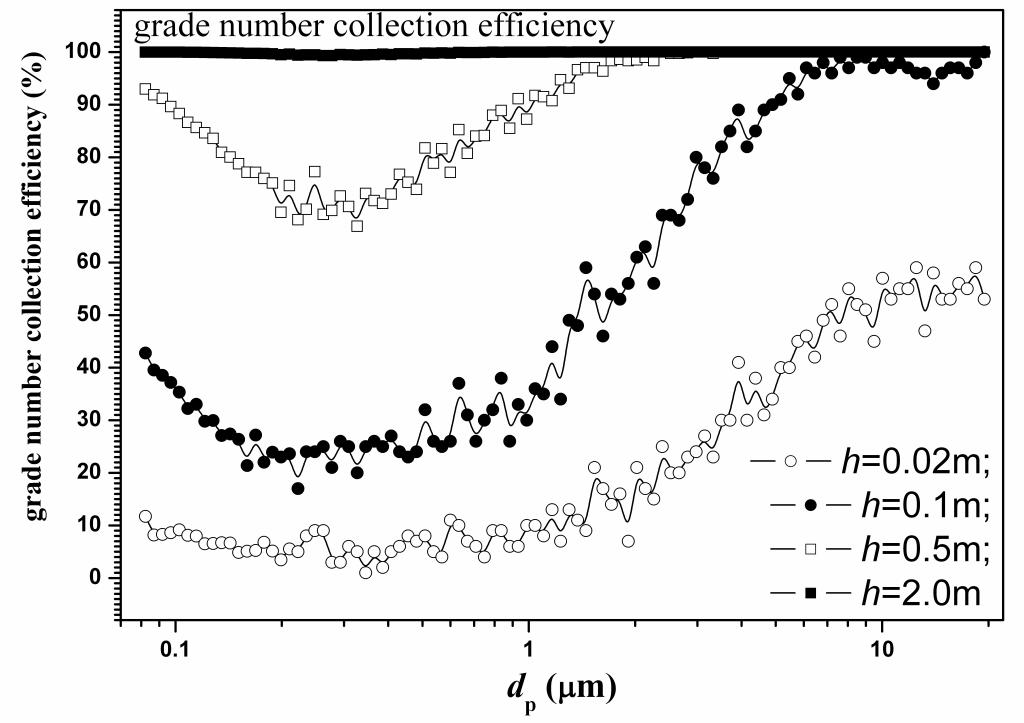
静电除尘器(左图)和静电增强湿式除尘器(右图)中燃煤可吸入颗粒物沉积规律

参考文献：

1. Haibo Zhao*, Chuguang Zheng. Modeling of Gravitational Wet Scrubbers with Electrostatic Enhancement. Chemical Engineering Technology, 2008, 31(12):1824–1837

2. Haibo Zhao*, Chuguang Zheng. A stochastic simulation for the collection process of fly ashes in single-stage electrostatic precipitators, Fuel, 2008, 87(10): 2082–2089

(8) 纤维捕集可吸入颗粒物的格子Boltzmann数值模拟

• 纤维捕集PM数值模拟的难点是沉积在纤维上的颗粒物也作为捕集介质，影响气固流场及随后的颗粒沉积，常规气固两相流模型难以处理这种复杂动态边界条件。采用格子Boltzmann-元胞自动机概率模型对常规圆形截面纤维、异形截面(椭圆形、矩形、三叶形、十字形、三角形等)纤维、多层纤维等稳态和动态纤维除尘过程进行多尺度模拟，揭示不同机理(布朗扩散、拦截、惯性碰撞)主导下压降、除尘效率、沉积模态、枝簇结构内部孔隙率等动态演变规律，指导布袋除尘器优化设计和运行。

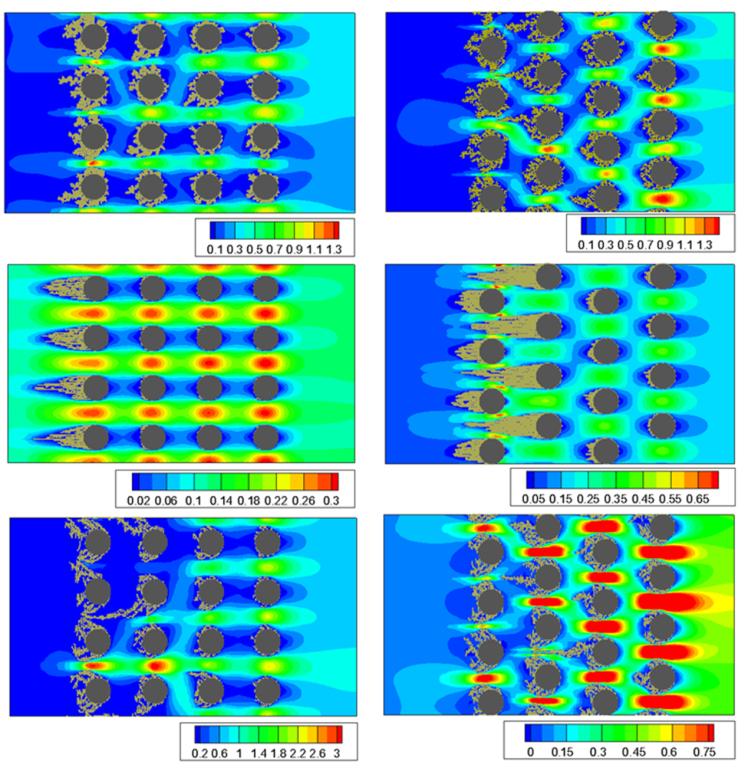
多层纤维捕集纳米颗粒过程(上：布朗扩散主导；中，惯性碰撞主导；下：拦截主导

参考文献：

1. Haoming Wang, Haibo Zhao^*, Zhaoli Guo, Chuguang Zheng. Numerical Simulation of Particle Capture Process of Fibrous Filters using Lattice Boltzmann Two-phase Flow Model. Powder Technology, 2012, 227: 111–122

2. Haoming Wang, Haibo Zhao^*, Kun Wang, Yongxiang He, Chuguang Zheng. Simulation of filtration process of multi-fiber filter using lattice-Boltzmann two-phase flow model. Journal of Aerosol Science, 2013, 66: 164-178

3. Kun Wang, Haibo Zhao^*. The influence of fiber geometry and orientation angle on its filtration performance. Aerosol Science and Technology, 2015, 49: 75-85

4. Haokai Huang, Kun Wang, Haibo Zhao^*. Numerical study of pressure drop and diffusional capture efficiency of several typical noncircular fibers in filtration. Powder Technology, 2016, 292: 232-241

5. Haoming Wang, Haibo Zhao^*, Kun Wang, Chuguang Zheng. Simulating and modeling particulate removal processes by elliptical fibers. Aerosol Science and Technology, 2014, 48(2): 207-218

6. Haokai Huang, Chaohe Zheng, Haibo Zhao*. Numerical investigation on particle loading process of elliptical fibers. Journal of Aerosol Science, 2017, in press

(9) 典型能源动力装置的数值模拟

• 对典型能源动力装置进行数值模拟将服务于常规/新型能源动力系统的燃烧效率、燃烧稳定性、污染物排放特征和控制方法、以及燃烧器、配风方式、烟气再循环方式等的设计和优化。流体-轨道模型和双流体模型各有优缺点。通过对开源代码进行再开发、基于商业软件进行用户自定义函数(UDF)编程等，对煤粉燃烧、循环流化床、撞击流煤气化炉等进行了数值模拟。例如，采用基于颗粒动理论的双流体模型对撞击流气化炉等进行了数值模拟，重点关注撞击面不稳定现象。

平面狭缝喷嘴气固撞击流的周期性震荡

参考文献：

1. Hongpeng Xu, Haibo Zhao*, Chuguang Zheng. Simulation and investigation of periodic deflecting oscillation of gas–solid planar opposed jets. Chemical Engineering and Processing: Process Intensification, 2014, 76: 6–15

2. Mingze Su, Haibo Zhao*, Jinchen Ma. Computational Fluid Dynamics Simulation for Chemical Looping Combustion of Coal in a Dual Circulation Fluidized Bed. Energy Conversion and Management, 2015, 105: 1–12.